Something relates to Computer Science and Technology, something relates to China and something I am not sure!
Saturday, June 30, 2012
Logging your stuffs, and prepared for rollback
Few weeks ago, I began to split the data into a number of fragments, and distributed them on different machines. Yesterday, I finished the code which could combine the separated data into one and perform the final step. It seems pretty good, but it is not... As it has been so long since the date I setup the first step, some critical configurations I made has became blurred. I suppose to remember those simple numbers which parsed into my programs, but it has been to late to correct me.
I lost about 20% of the data, which may need another few weeks to recover.
So, I suggest that, every one should keep a simple log, to record some crucial information you may need in the future, such as what/when/how you have done. Even it is not exact you need, it could help you to remember at least.
Thursday, June 28, 2012
How to create a program to handle HUGE data?[0]
In the following posts, I will discuss what I have suffered during the development, what I have applied to the system, and what I want to do but have not done yet. All the topics which gonna be covered can be classified into two categories, design philosophy and design pattern.
... to be continued...
Tuesday, June 26, 2012
Saturday, June 23, 2012
Maximal matching of bipartite graph
There are mainly two methods to find maximal matching, max flow algorithm and Hungarian algorithm. Hungarian algorithm use the idea behind max flow algorithm, but simplified the max flow algorithm based on the properties of bipartite matching and improve the performance.
Before we read those algorithm, another definition need to be clarified, augmenting path. If P is the path that connects two unmatched nodes, and the nodes in M and not M appear alternately, then we call P is a augmenting path on M. Then we could generalize 4 conclusions as follows:
- The length of P must be odd; the first edge and the last edge should not belongs to M;
- All the odd number edges are not in M, and all the even number edges are in M;
- A bigger match M` could be found by “invert” P. Here, “invert” means put all odd number edges into M, and remove all even number edges in P from M. So there must be one more match.
- M is the maximal match, if and only if, there is not augmenting path in G;
Initialize the Maximal Match, MM, as null; while( augmenting path exists ) { Add the augmenting path into MM; }The main idea of the algorithm above is keeping searching augmenting paths, which could increase the number of matching. In matching problem, augmenting path looks like a zigzag. If the first edge of a graph does not in match, its second edge should be in, and so on. If we could invert the selection of matches, we could find one more match legally.
Further Properties:
- Minimal covering: find the minimal set of node, m, and make each edge connects to an arbitrary node in m. So,
- The minimal path covering = |N| – maximal match.
Use minimal number of unoverlapping edges cover all the nodes in the graph, G. We could build up a bipartite model. All the nodes are divided into two sets, X and Y. If there is a edge i->j, then we add edge(i->j`). If the maximal match is m, then the result is n-m;
- Max independent set = (node number) – (bipartite maximal match)
In a graph which have N nodes, we select m nodes, and each pair of the m nodes are not connected. Then find the maximal m. If G satisfies bipartite, then we could use bipartite matching to find result, as the minimal path covering = |N| – maximal match
Friday, June 22, 2012
Running on linked list :)
Question 1: find the last K node of a given linked list;
Suppose you have a singly linked list L, please return the last K node in the list.
Solution: this problem is trivial. We could define two pointers, p1 and p2. We move p1 to the K-th node in the list and then move both pointers to the end node concurrently. Once p1 reaches the end, p2 points to the last K-th node.
Question 2: How to detect two linked lists merge or not;
Suppose you have two singly linked list, L1 and L2. Return true if those two lists merge at a arbitrary node; otherwise, return false.
Solution: This question is also trivial. If two lists merge, the end node must be the same. If we go through those two lists and end at the some node, we return true. Otherwise, they do not merge.
The method mentioned above need an assumption, there is no loop in both lists. If there is a loop, the method above will not work. If we could detect whether a loop is in the list, we could have the following generic algorithm to determine the return value.
detect loop
if no loop in both list, compare the end node;
if there are loops, check the node in one loop. If it is also in other loop, then they merge; otherwise, then do not.
Question 3: How to detect loops in a linked list;
Give you a singly LL, detect whether there is a loop in it.
Solution: the answer to this problem is really interesting. We could define two pointer, Fast and Slow. Fast pointer moves two nodes per time and Slow move one step each time. If there is a loop, those two pointers will meet in a position in the loop. In order to make the correctness easier, we assume that the length of the linked is upper bounded. We move the pointers until touch the upper bounder, which could guarantee we wont stop before enter the loop.
If we move this question a little further, how to find the beginning of the loop? Suppose the LL looks as follows:

The speed of those two pointers are 2 and 1. when they meet, if the total length of Slow moved is S, the Fast should have moved 2S. In addition, Fast moved n loops more. If the length of loop is r, we have nr = S. S can be replaced by a + x, the distance between loop enter point and meet point. So we have:
a + x = nr = ( n - 1 )r + L - a Then: a = ( n - 1 )r + ( L - a - x )
( L-a-x ) is the length between the meet point and the next loop enter point. So, if release another two pointers, Slow, at first node and meet point, they must meet at enter point of the loop, as ( n –1 )r will be cancelled by the loop.
Question 4: There is a straight track on the ground. Two robots randomly placed on the track. You need to deploy program on both robots. By executing the same program, they must collide each other.( This is a real interview question from Microsoft Advanced Technology Center in China )
There are four instructions in the instruction set:
- go left
- go right
- check. Return true if the other robot visited current position, otherwise, return false;
- jump, jump to any position in the program;
start:
if(at the position other robots have not reached)
move_right
if(at the position other robots have reached)
move_right
move_right
goto start
The idea of this algorithm is initiative. If one robot found the other one is in front of it( the position visited by the other robot ), it runs faster to catch up.
Thursday, June 21, 2012
Dynamic programming
Dynamic programming, or DP for short, can be applied on the problems that could be divided into sub problems. The solution of the entire problem can be found by “combing” the solutions of its sub problem. The main steps of DP can be generalized as follows:
- define the solution;
- recursively define the solutions from sub solution;
- calculate the solution, from bottom to the top;
- generate a solution based on the sub-solutions.
There are two key points needed to be clarified, before applying DP. The first is optimal substructure and the other one is overlapping sub problems.
- Optimal substructure, means the substructures of a solution must be also optimal;
- Overlapping sub problem, means the sub problems, when we recursively decompose the problem, may not be always new problems. For example, some problems may need to be calculated many times. If we could store the result of it, then we could just lookup the result, instead of recalculating. In another world, DP is a method which uses space to reduce time.
Now, let us check a typical DP problem, longest common subsequence(LCS). If you do not know LCS, please Google it.
Suppose there are two string, Xm={x1, x2, x3, …, xm} and Yn={y1, y2, y3, …, yn}. Zk={z1, z2, z3, …, zk} is the X`s, or Y`s, LCS. The elements in LCS need to be in the same order, but not continuous.
Then we could find three properties as follows:
- if xm-1 == yn-1, then zk-1 = xm-1 == yn-1, and zk-1 is a LCS of Xm-1 and Yn-1;
- if xm-1 != yn-1, and zk-1 != xm-1, Z is the LCS of xm-1 and Y;
- if xm-1 != yn-1, and zk-1 != yn-1, Z is the LCS of yn-1 and X;
A recursive solution could be obtained as follows. Suppose c[m][n] denotes the length of the LSC of X[1:m] and Y[1:n].
/ 0, if i<0 and j<0; // case 1
c[i][j] = | c[i-1][j-1]+1, if i, j >=0 and xi==yj; // case 2
\ max( c[i][j-1]m c[i-1][j] ), if i, j>=0 and xi!=yj; // case 3
After we execute the function above recursively, we could found the length of LCS at c[m][n]. If we want extract the LCS, we need to define anther matrix, D, to store the direction of how each state transited, and define 3 three directions.
- If D[i][j] holds direction 1, denoted as
, we move next position at D[i-1][j-1];
- If D[i][j] holds direction 2, denoted as
, we move next position at D[i-1][j];
- If D[i][j] holds direction 3, denoted as
,we move next position at D[i][j-1];
Those three directions correspond to the conditions in the case 2 and 3 in the function. A trace back function as followed could be used to print the LCS. Suppose b is one string, X is the direction map and (i, j) is the index of X.
Wednesday, June 20, 2012
胤祉如是,吾似胤祉
动态规划之背包问题【3】
背包问题的下一个变体是二维背包问题!
二维背包问题的描述如下:对于每件物品,具有两种不同的费用;选择这件物品必须同时付出这两种代价;对于每种代价都有一个可付出的最大值(背包容量)。问怎样选择物品可以得到最大的价值。设这两种代价分别为代价1和代价2,第i件物品所需的两种代价分别为a[i]和b[i]。两种代价可付出的最大值(两种背包容量)分别为V和U。物品的价值为w[i]。
他的解法很直接,因为状态多了一维,可以在状态上加一维!假设f[i][u][v]为前i个物品,且付出u和v费用时的最大价值!状态转移方程如下:
f[i][v][u]=max( f[i-1][v][u], f[i-1][v-a[i]][u-b[i]]+w[i] );
上面这个方程的空间复杂度是O(N^3),我们可以用01背包中那个逆向循环的办法,把三维的方程转化成二维的。
应对总个数的限制
“二维费用”的条件有时是以这样一种隐含的方式给出的:最多只能取M件物品。这事实上相当于每件物品多了一种“件数”的费用,每个物品的件数费用均为1,可以付出的最大件数费用为M。换句话说,设f[v][m]表示付出费用v、最多选m件时可得到的最大价值,则根据物品的类型(01、完全、多重)用不同的方法循环更新,最后在f[0..V][0..M]范围内寻找答案。【Source】
所以,当发现由熟悉的动态规划题目变形得来的题目时,在原来的状态中加一纬以满足新的限制是一种比较通用的方法。
下面给出一个二维背包的题目:
Description
The NASA Space Center, Houston, is less than 200 miles from San Antonio, Texas (the site of the ACM Finals this year). This is the place where the astronauts are trained for Mission Seven Dwarfs, the next giant leap in space exploration. The Mars Odyssey program revealed that the surface of Mars is very rich in yeyenum and bloggium. These minerals are important ingredients for certain revolutionary new medicines, but they are extremely rare on Earth. The aim of Mission Seven Dwarfs is to mine these minerals on Mars and bring them back to Earth.
The Mars Odyssey orbiter identified a rectangular area on the surface of Mars that is rich in minerals. The area is divided into cells that form a matrix of n rows and m columns, where the rows go from east to west and the columns go from north to south. The orbiter determined the amount of yeyenum and bloggium in each cell. The astronauts will build a yeyenum refinement factory west of the rectangular area and a bloggium factory to the north. Your task is to design the conveyor belt system that will allow them to mine the largest amount of minerals.
There are two types of conveyor belts: the first moves minerals from east to west, the second moves minerals from south to north. In each cell you can build either type of conveyor belt, but you cannot build both of them in the same cell. If two conveyor belts of the same type are next to each other, then they can be connected. For example, the bloggium mined at a cell can be transported to the bloggium refinement factory via a series of south-north conveyor belts.
The minerals are very unstable, thus they have to be brought to the factories on a straight path without any turns. This means that if there is a south-north conveyor belt in a cell, but the cell north of it contains an east-west conveyor belt, then any mineral transported on the south-north conveyor beltwill be lost. The minerals mined in a particular cell have to be put on a conveyor belt immediately, in the same cell (thus they cannot start the transportation in an adjacent cell). Furthermore, any bloggium transported to the yeyenum refinement factory will be lost, and vice versa.
Your program has to design a conveyor belt system that maximizes the total amount of minerals mined,i.e., the sum of the amount of yeyenum transported to the yeyenum refinery and the amount of bloggium transported to the bloggium refinery.
Input
The input contains several blocks of test cases. Each case begins with a line containing two integers: the number 1 ≤ n ≤ 500 of rows, and the number 1 ≤ m ≤ 500 of columns. The next n lines describe the amount of yeyenum that can be found in the cells. Each of these n lines contains m integers. The first line corresponds to the northernmost row; the first integer of each line corresponds to the westernmost cell of the row. The integers are between 0 and 1000. The next n lines describe in a similar fashion theamount of bloggium found in the cells.
The input is terminated by a block with n = m = 0.
Output
For each test case, you have to output a single integer on a separate line: the maximum amount of mineralsthat can be mined.
Sample Input
4 4
0 0 10 9
1 3 10 0
4 2 1 3
1 1 20 0
10 0 0 0
1 1 1 30
0 0 5 5
5 10 10 10
0 0
Sample Output
98
Hint
Huge input file, 'scanf' recommended to avoid TLE.
Source: Central Europe 2005
这个题目很经典,而且已经有了不少代码了解决这个问题!下面我给出我的思路,代码稍后会给出!
假设在某个状态i,整个系统的解可以由状态i-1得出,可以看下图:
As we could see from this figure. In state i-1, each block, marked by black, may have a N wealth, or W wealth, or both. In iteration i, we need to decide the transportation for the position marked by red and where the blue arrows placed. The red block can either be W or N. Because no matter what we place there, the new result will not bad than the previous one. If we place a W convey path in the red block, the blocks lower than it will be W for sure. Then, we only need to consider the W convey path, from the red block, ends at which block on the right. For example, if the red block points to N, all the path on right should be to N. The only variable here is the path to N, on i-th column, ends at which block. If it ends at K, all the wealth in i-1 to W of top K blocks is omitted. At the same time, K blocks of wealth to N is added to the total wealth. We need to find the value of K and the direction of the red block.
We could write a state transaction formula as follows:
wealth[i] = max( argmaxi<k<width( wealth[i-1] – sum( wealth to N, from i to K ) + sum( wealth to W on i row, from i to K ) ), argmaxi<k<height( wealth[i-1] – sum( wealth to W, from i to K ) + sum( wealth to N on i column, from i to K ) ) );
Tuesday, June 19, 2012
微软平板电脑需要的是自己来证明自己
动态规划之背包问题【2】
背包问题的另一个代表是完全背包问题,就是可放的物品有无穷多个,你可以重复选择!所以问题的描述就变成了:
有N种物品和一个容量为V的背包,每种物品都有无限件可用。第i种物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
如果按传统01背包的思路来考虑,我们可以得到如下的状态转移方程:
f[i][v] = max{ f[i-1][v-k*c[i]]+k*w[i] }, where 0<=k*c[i]<=v;上面的这个方程相当于在01背包原有基础上,在加上一个循环,将第i个物品可能放的数目都实验一遍!所以对应的状态还是O(VN)个,但每个状态的求解时间变成了O(v/c[i]),总的复杂度变成了O(V*Sum(V/c[i]))!
对于上面的这种情况,我们可以考虑一个简单的优化办法!
将符合c[i]<=c[j],w[i]>=w[j]的物品删掉!这个优化显然正确,因为我们总能用c[i]来替换c[j],得到的结果至少不比原来的结果差!但要注意,我们不能用密度来替换,那样就犯了贪心算法的错误!例如三个物品:c1=49,c2=50,c3=51;v1=1,v2=2,v3=2.5…明显得不到正确结果!
下面说两个复杂点的优化方法,我给他们起了两个名字方便大家记忆:一个是平铺,一个是2进制编码!下面我分别分析一下!
平铺的核心思想就是将物品提前重复,因为第i个物品最多放v/c[i]次,那我们就重复放v/c[i]个物品在可选的物品集合里,这样,虽然物品的数量大了,而且有重复,但我们就能直接用01背包的算法求解了!
2进制编码的核心思想跟十进制转二进制数类似。将第i个物品转化为若干个物品,其中新的价值为w[i]*2^k;新的费用为c[i]*2^k,其中k满足c[i]*2^k<=V。这样,不管我们重复选几个c[i],都会有一个或多个新物品的组合与之对应!并可以轻松的求出c[i]需要的次数!
下面在介绍一个O(VN)算法!
这个算法使用一维数组,先看伪代码:
for i=1..N
for v=0..V
f[v]=max{f[v],f[v-cost]+weight}
你会发现,这个伪代码与01背包空间优化算法伪代码只有v的循环次序不同而已。按照v=V..0的逆序来循环,是为了保证第i次循环中的状态f[i][v]是由状态f[i-1][v-c[i]]递推而来。换句话说,这正是为了保证每件物品只选一次,保证在考虑“选入第i件物品”这件策略时,依据的是一个绝无已经选入第i件物品的子结果f[i-1][v-c[i]]。而现在完全背包的特点恰是每种物品可选无限件,所以在考虑“加选一件第i种物品”这种策略时,却正需要一个可能已选入第i种物品的子结果f[i][v-c[i]],所以就可以并且必须采用v=0..V的顺序循环。上面的这个思路,可以得到一个改进的状态转移方程,如下:
f[i][v]=max{f[i-1][v],f[i][v-c[i]]+w[i]}
Monday, June 18, 2012
动态规划之背包问题【1】
01背包问题
问题:有N件物品和一个容量为V的背包。第i件物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使价值总和最大。
状态转移方程:f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}
其中f[i][v]表示前i个物品恰好放在容量为v的背包里所能获得的最大价值。这个方程的核心就是:第i个物品放与不放的问题,可以转化为一个只牵扯前i-1件物品的问题。
- 如果放第i个物品,则转化为“前i-1个物品放入容量为v-c[i]的背包中”问题,其价值等于w[i]+f[i-1][v-c[i]];
- 如果第i个物品不放,则转化为“前i-1个物品放入v的背包中”的问题,其价值等于f[i-1][v];
1: Backpack( N, v, C, W )
2: {
3: initialize 2D-array f[N.size][v]
4: for i=1 to N.size
5: {
6: for vv=1 to v
7: {
8: f[i][vv] = max{ f[i-1][vv], f[i-1][vv-C[i]]+W[i] };
9: }
10: }
11: }
1: Backpack( N, v, C, W )
2: {
3: initialize 1D-array f[v]
4: for i=1 to N.size
5: {
6: // as the item i, which has C[i], will not
7: // affect f[0 to C[i]-1]. If it happend,
8: // the index will exceed the lower boundary.
9: for vv=v to C[i]
10: {
11: f[vv]=max{f[vv],f[vv-C[i]]+W[i]};
12: }
13: }
14: }
Sunday, June 17, 2012
Are you a nerd? No, I am coding ninja!
但我要说我得到了另一个世界!
有人说你已经学成了书呆子,
但我要说我找到了更值得我关心的东西!
有人说你这样下去找不到女朋友,
但我要说我有一个永不背叛的soul mate!
有人说你已经彻底疯了,
但我要说,老子是编代码的,不培养这样的性格,怎么写代码,debug,查异常!
I am a nerd? No, I am coding ninja!
为了完成自己的工作,不得已把脸蒙起来!
然后就不习惯摘下来了!
Saturday, June 16, 2012
最短路径算法
给你 n 个点,m 条无向边,每条边都有长度 d 和花费 p,给你起点 s 终点 t,要求输出
起点到终点的最短距离及其花费,如果最短距离有多条路线,则输出花费最少的。
输入:输入 n , m,点的编号是 1~n,然后是 m 行,每行 4 个数 a,b,d,p,表示 a 和 b
之间有一条边,且其长度为 d,花费为 p。最后一行是两个数 s,t;起点 s,终点 t。n 和 m
为 0 时输入结束。(1
输出:一行有两个数,最短距离及其花费。
This is a typical shortest path problem. We could solve it with three methods, Dijkstra algorithm, Dellman-Ford algorithm and Shortest Path Faster Algorithm. In the following sections, pseudo codes are listed.
Dijkstra Algorithm:
1: void Dijkstra( Graph, source )
2: {
3: // Initialization
4: foreach vertex v in Graph
5: {
6: // set the distances to infinity
7: dist[v] = infinity;
8: // set each node with no previouse node
9: previous[v] = undefined;
10: }
11: // source node has no ditance to itself
12: dist[source] = 0;
13: // Q is a set that contains all the nodes in Graph
14: Q = Graph.nodes;
15: // travse
16: while( Q is not empty )
17: {
18: // pop a node from Q which has the smallest distance
19: // to the source node
20: u = vertex in Q with smallest distance in dist[];
21: // if the nearest node is infinity, there should be no
22: // more nodes coule be updated
23: if( dist[u] = infinity )
24: {
25: break;
26: }
27: // the node should not be update twice
28: remove u from Q;
29: // update all the neighbor nodes of current node
30: foreach neighbor v of u
31: {
32: // calculte a temp path, which go though current
33: // u, to v
34: alt = dist[u] + dist_between(u, v);
35: // if the temp path is shorter, update
36: if( alt < dist[v] )
37: {
38: dist[v] = alt;
39: previous[v] = u;
40: reorder v in Q
41: }
42: }
43: }
44: //
45: // dist[] holds the distance
46: // and previous[] contains the previous node
47: // in a shortest path
48: //
49: }
Bellman-Ford Algorithm:
1: void BellmanFord( Graph, source )
2: {
3: // initialize
4: foreach vertex v in Graph.vertices
5: {
6: // set the initial distance
7: if( v is source )
8: {
9: // source node is 0
10: v.distance = 0;
11: }
12: else
13: {
14: // the others are infinity
15: v.distance = infinity;
16: }
17: // no previous node in the shortest path
18: v.previous = null;
19: }
20: // relax the edges
21: for i from 1 to Graph.vertices.size-1
22: {
23: // update the distance, suppose a path goes
24: // from source and ends at u
25: foreach edge uv in Graph.edges
26: {
27: u = uv.source;
28: v = uv.destination;
29: // if the path is shorter than the previous
30: // path, update
31: if( u.distance+uv.weight < v.distance )
32: {
33: v.distance = u.distance + uv.weight;
34: v.previous = u;
35: }
36: }
37: }
38: // check the negative-weight cycles
39: // if such cycles exist, the result is worry
40: foreach edge uv in Graph.edges
41: {
42: u = uv.source;
43: v = uv.destination;
44: // negative circle
45: if( u.distance + uv.weight < v.distance )
46: {
47: print error;
48: exit;
49: }
50: }
51: return;
52: }
SPFA Algorithm:
1: void BellmanFord( Graph, source )
2: {
3: // initialize
4: foreach vertex v in Graph.vertices
5: {
6: // set the initial distance
7: if( v is source )
8: {
9: // source node is 0
10: v.distance = 0;
11: }
12: else
13: {
14: // the others are infinity
15: v.distance = infinity;
16: }
17: // no previous node in the shortest path
18: v.previous = null;
19: }
20: // relax the edges
21: for i from 1 to Graph.vertices.size-1
22: {
23: // update the distance, suppose a path goes
24: // from source and ends at u
25: foreach edge uv in Graph.edges
26: {
27: u = uv.source;
28: v = uv.destination;
29: // if the path is shorter than the previous
30: // path, update
31: if( u.distance+uv.weight < v.distance )
32: {
33: v.distance = u.distance + uv.weight;
34: v.previous = u;
35: }
36: }
37: }
38: // check the negative-weight cycles
39: // if such cycles exist, the result is worry
40: foreach edge uv in Graph.edges
41: {
42: u = uv.source;
43: v = uv.destination;
44: // negative circle
45: if( u.distance + uv.weight < v.distance )
46: {
47: print error;
48: exit;
49: }
50: }
51: return;
52: }
Wednesday, June 13, 2012
面向对象编程有感【2】-- Understand SRP and LSP
Requirement: We need to design a web spider, which could traverse all the web pages rooted from a seed link. There are a number of different types of pages, which need different operation to be performed. In addition, we may have to add more types in the future.
After you reading the simple description above, few design patterns may pop up in your mind, such as factory pattern, responsibility chain pattern, observer pattern, MVC pattern and singleton pattern. Right, all those patterns are designed to assist you in such a scenario. But, when you implement all the patterns together, there may be few mistakes happened. Let us take a look at my code first.
I defined few classes as follows:
- BaseTask and its subclasses. The base class has few virtual functions, which generalize some common operations needed by each types of page.
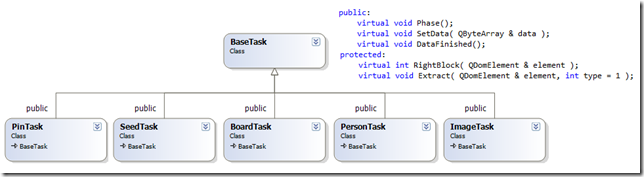
- pObject and its subcalsses. As the data extracted from the pages may have different saving path and preprocessing requirement. pObject opens few virtual functions, such as where to save the data and how to preprocess it. Its derivatives override those functions and properly handle/keep the data.
- The next two classes are Download_Manager and Data_Manager. Download_Manager is the observer to the Data_Manager. Once a new task, which is in form of BaseTask, is added to Data_Manager, Download_Manager will try to pop the task from the task queue and download the page needed by this task. Once the page is downloaded, it will be assigned to the task and the task will return to Data_Manager, where the analyzing is performed. Some new tasks may be initialized and append to Data_Manager during analyzing. Furthermore, Singleton pattern is applied to both managers, so only few interfaces are opened to each other.
The reason why I design like this is that, the only object transferred between managers is BaseTask. So if we want to handle other types of pages, we could just implement another derivative class and push the objects into the task queue. In addition, each task has a “pObject”, which could handle the file path, URL and analyze process.
- Inside each task object, as we need to open a constant interface to other components, I define a recursive function, called decompose(), which is used to traverse all XML blocks and allow other parts to invoke. The code segment looks like the follows:
1: void BaseTask::Decompose( QDomElement parentElement )
2: {
3: QDomNode element = parentElement.firstChild();
4: //
5: while(!element.isNull())
6: {
7: int type = this->RightBlock( element.toElement() );
8: if( type!=0 )
9: {
10: Extract( element.toElement(), type );
11: }
12: Decompose( element.toElement() );
13: element = element.nextSibling();
14: }
15: return;
16: }
RightBlock() is used to determine which XML block is needed; Extract() is used to extract the information in the XML block. Each derivative class will override those two functions, and then, each object of derivative class will act in different ways. The following flow chart shows how this code works.
This is a common trick in C++ based on polymorphism. We could initialize an object with sub-class but assign it to a base class pointer. As the functions in base class are virtual, the function point in virtual function table will updated to the implementation in subclass.
So far so good, right. LSP seems applied properly. But I found a big mistake about SRP when I try to update the code. Which part violates SRP? Let us first understand what I want to update with the original architecture.
As my previous structure tries to do everything in one executable, it becomes very vulnerable, or buggy. So I want to add a simple function that could resume the previous downloading. It seems simple but it is not. Because the tasks does not follow SRP. Let us first examine what happened inside a task object from its creation to release.
Can you find which part is worry? Right, the file system and URL interface is only a variable of the task objects. When I want to recover the downloading, the program may not need to download the page, but directly start the parsing. But based on the above sequence, the tasks are initialized by other tasks during parsing; parsing begins after download is finished; we want to recover and omit the download step… Now, you see the dead loop right. If we add more if-else, the original code may work, but not elegant.
Another part looking ugly is the URL interface. As the relative paths need to be translated into global, we not only need its parent object, but also modify the format. For example, the hierarchy of a website is as follows:
- First level, front page. The URL is www.pinterest.com
- Second level, user page, which contains a number of image folders. The URL is www.pinterest.com/user_name
- Third level, image folder, which holds a number images. The URL is www.pinterest.com/user_name/pin_board
- The final level, the images. The URL is www.pinterest.com/pin/pin_id
Each task object need to perform modification respectively. If I put the modification in tasks, it is easier and straight forward, but the code is hard to maintain. Imagine such a situation, all the levels of URL are updated and what shall we do? Update all relevant code in each subclass of BaseTask? What if we have 100 different tasks? It is not possible… The pObject in also lost its meaning of existence. As SRP says, we should put one responsibility in one object! We should put all URLs and paths task in pObject. The following diagram shows what the code should look like.
My previous design of the tasks looks like the left diagram. When the URLs input to task, there are more than one object could modify it. So it undermined the scalability of the code. The right hand diagram shows a design that keeps both scalability and the same functionalities. You feel familiar with the right hand side diagram. Because it likes the responsibility chain pattern, from some point of view. If any parts updated, you could just plugin another object to filter the input, and isolate the changes to the other component.
I have written so much. As I am also a green hand of this topic, some mistakes and errors may occur. If you found any, or just want to share your idea, please leave me a comment or directly email me.
Have fun!
Sunday, June 10, 2012
面向对象编程有感【1】--基本原则
在面向对象设计中,如何通过很小的设计改变就可以应对设计需求的变化,这是令设计者极为关注的问题。为此不少OO先驱提出了很多有关面向对象的设计原则用于指导OO的设计和开发。下面是几条与类设计相关的设计原则。
单一职责原则SRP:Single Responsibility Principle
开放封闭原则OCP:Open-Close Principle
Liskov替换原则LSP:Liskov Substitution Principle
依赖倒置原则DIP:Dependency Invertion Principle
接口隔离原则ISP:Interface Separate Principle
在面向对象设计中,如何通过很小的设计改变就可以应对设计需求的变化,这是令设计者极为关注的问题。为此不少OO先驱提出了很多有关面向对象的设计原则用于指导OO的设计和开发。下面是几条与类设计相关的设计原则。
1. 开闭原则(the Open Closed Principle OCP)
一个模块在扩展性方面应该是开放的而在更改性方面应该是封闭的。因此在进行面向对象设计时要尽量考虑接口封装机制、抽象机制和多态技术。该原则同样适合于非面向对象设计的方法,是软件工程设计方法的重要原则之一。我们以收音机的例子为例,讲述面向对象的开闭原则。我们收听节目时需要打开收音机电源,对准电台频率和进行音量调节。但是对于不同的收音机,实现这三个步骤的细节往往有所不同。比如自动收缩电台的收音机和按钮式收缩在操作细节上并不相同。因此,我们不太可能针对每种不同类型的收音机通过一个收音机类来实现(通过重载)这些不同的操作方式。但是我们可以定义一个收音机接口,提供开机、关机、增加频率、降低频率、增加音量、降低音量六个抽象方法。不同的收音机继承并实现这六个抽象方法。这样新增收音机类型不会影响其它原有的收音机类型,收音机类型扩展极为方便。此外,已存在的收音机类型在修改其操作方法时也不会影响到其它类型的收音机。
2. 替换原则 (the Liskov Substitution Principle LSP)
子类应当可以替换父类并出现在父类能够出现的任何地方。这个原则是Liskov于1987年提出的设计原则。它同样可以从Bertrand Meyer 的DBC (Design by Contract) 的概念推出。
我们以学生为例,夜校生为学生的子类,因此在任何学生可以出现的地方,夜校生均可出现。这个例子有些牵强,一个能够反映这个原则的例子时圆和椭圆,圆是椭圆的一个特殊子类。因此任何出现椭圆的地方,圆均可以出现。但反过来就可能行不通。
运用替换原则时,我们尽量把类B设计为抽象类或者接口,让C类继承类B(接口B)并实现操作A和操作B,运行时,类C实例替换B,这样我们即可进行新类的扩展(继承类B或接口B),同时无须对类A进行修改。
3. 依赖原则 (the Dependency Inversion Principle DIP)
在进行业务设计时,与特定业务有关的依赖关系应该尽量依赖接口和抽象类,而不是依赖于具体类。具体类只负责相关业务的实现,修改具体类不影响与特定业务有关的依赖关系。
在结构化设计中,我们可以看到底层的模块是对高层抽象模块的实现(高层抽象模块通过调用底层模块),这说明,抽象的模块要依赖具体实现相关的模块,底层模块的具体实现发生变动时将会严重影响高层抽象的模块,显然这是结构化方法的一个"硬伤"。
面向对象方法的依赖关系刚好相反,具体实现类依赖于抽象类和接口。
为此,我们在进行业务设计时,应尽量在接口或抽象类中定义业务方法的原型,并通过具体的实现类(子类)来实现该业务方法,业务方法内容的修改将不会影响到运行时业务方法的调用。
4. 接口分离原则(the Interface Segregation Principle ISP)
采用多个与特定客户类有关的接口比采用一个通用的涵盖多个业务方法的接口要好。
ISP原则是另外一个支持诸如COM等组件化的使能技术。缺少ISP,组件、类的可用性和移植性将大打折扣。
这个原则的本质相当简单。如果你拥有一个针对多个客户的类,为每一个客户创建特定业务接口,然后使该客户类继承多个特定业务接口将比直接加载客户所需所有方法有效。
以上四个原则是面向对象中常常用到的原则。此外,除上述四原则外,还有一些常用的经验诸如类结构层次以三到四层为宜、类的职责明确化(一个类对应一个具体职责)等可供我们在进行面向对象设计参考。但就上面的几个原则看来,我们看到这些类在几何分布上呈现树型拓扑的关系,这是一种良好、开放式的线性关系、具有较低的设计复杂度。一般说来,在软件设计中我们应当尽量避免出现带有闭包、循环的设计关系,它们反映的是较大的耦合度和设计复杂化。
Monday, June 4, 2012
How to define a function pointer to a member function of an object
As the member functions depend on object, the point of a non-static function is actually an offset.
1: class A
2: {
3: int _val;
4: int val();
5: };
6:
7: int (A::*p_val) = &A::_val;
8: int ( A::*p_func )() = &A::val;
Pointer to static member function. As static function of a class does not depend on any object of that class, the pointer is the same as the one in C.
1: class A
2: {
3: static int _val;
4: static int val();
5: };
6:
7: int *p_val = &A::_val;
8: int (*p_func) = &A::val;
Advantages: 1. easy to call; 2. callback function
A complete example:
1: #include <iostream>
2: #include <string>
3: using namespace std;
4:
5: typedef void (*funchandler)();
6:
7: void register_func(funchandler f)
8: {
9: cout << "register_func" << endl;
10: (*f)();
11: }
12:
13: class A
14: {
15: public:
16: A() : _val( 0 ) { cout << "create A..." << endl; }
17: void test() { cout << "test..." << endl; }
18: void test1() { cout << "test1..." << endl; }
19: void test2() { cout << "test2..." << endl; }
20: int val() { return _val; }
21: static void test3() { cout << "test3..." << endl; }
22: int _val;
23: private:
24: };
25:
26: int main()
27: {
28: A a;
29: int ( A::*p_val ) = 0;
30: p_val = &A::_val;
31: cout << "a.*p_val: " << a.*p_val << endl;
32:
33: void (A::*p_func)();
34: p_func = &A::test;
35:
36: a.test();
37: (a.*p_func)();
38:
39: p_func = &A::test1;
40: ( a.*p_func )();
41: p_func = &A::test2;
42: ( a.*p_func )();
43:
44: void (* pp_func)();
45: pp_func = &A::test3;
46: (*pp_func)();
47:
48: register_func( pp_func );
49: return 0;
50: }
Friday, June 1, 2012
Programming with PowerShell, or not?
One possible solution is PowerShell, which is very powerful on Windows. I wrote the following code:
1: # checks the number of inputs and only accepts one input
2: if( $args.Count -ne 1 )
3: {
4: # print usage information
5: Write-Host "Usage:" $MyInvocation.MyCommand.Name "path"
6: # exit
7: exit
8: }
9: # the first input is the path to the targeting directory
10: $directory = $args[0]
11: # find the number of sub-directories
12: $folders = Get-ChildItem $directory;
13: Write-Host $folders
14: # a fixed step size, which is 10
15: $step = 10
16: # checks all the sub-folders, such as 10 to 10+10, or 30 to 30+10
17: for($from=0; $from -lt $folders.Count; $from=$from+$step)
18: {
19: $to = $to+$step
20: # call my code and pass the parameters
21: ./WebSpider.exe $directory 2000 1 $from $to
22: }
When I want to run the script, there is an error popped up, which says the script file cannot be load because the execution of script is disabled. WTF… Are you guys at Microsoft kidding me?! You implemented a shell interface, but disabled it to users?! You need administrator authority to enable it by the following command, otherwise, you cannot run scripts with PowerShell.
Set-ExecutionPolicy RemoteSigned
UPDATE:
Powershell -ExecutionPolicy RemoteSigned
The students, like me, do not have administrator authority on the desktops in the lab. So I cannot use the scripted…
Finally, I decide to rewrite a batch version instead.
1: @echo off
2: IF "%1"=="" goto stop
3: set path=%1
4: echo %1%
5: set start=0
6: set step=10
7: rem count the number of folders
8: setlocal EnableDelayedExpansion
9: set /a count=0
10: for /d %%d in (%path%*) do (
11: set /a count+=1
12: rem @echo !count!. %%d
13: )
14: set /a end=%count%
15: ECHO Folder %end%
16: :loop
17: if %start% GTR %end% goto stop
18: set /a cur = %start%+%step%
19:
20: rem echo from %start% to %cur%
21: rem run the code
22: WebSpider.exe 2000 1 %start% %step% %1%
23:
24: set /a start = %cur%
25: goto loop
26: :stop
27: rem
I used to admit PowerShell very much, for its integration with DotNet and extendable command-let. However, I just cannot understand why Microsoft disables his own product by default?! You may argue that the users on Windows may make mistake and … It does not make any scene, either. If a shell interface cannot run script, can you find any other functionalities we need, from a shell?!
我们歌唱黄河
by 郭小川, 1940年5月4日陕北绥德
我们在河边上住了几百代,
我们对黄河有着最深的乡土爱,
我们知道河边上
有多少村庄,
多少山崖;
我们知道
什么时候浪头高,
什么时候山水来;
我们歌唱黄河,
也歌唱我们的乡土爱。
来呀,
今天这样好日子,
为什么不唱起来!
来呀,
今天这样好日子,
你还把谁等待!
来呀,
你们这脸上没有胡子的,
额上没有皱纹的,
这正是我们歌唱的时代!
来呀,
你们这和强盗厮杀的战士们,
和浪涛搏斗的水手们,
和土地拼命的农民们,
大胆地跳上舞台!
唱吧,
今儿天上没有阴霾,
我爱呼吸就呼吸个痛快;
今儿天上缀满星星,
给我们生命无限的光采;
今儿这广大的黄河西岸
是你的舞台,
是我的舞台,
是大家的舞台。
唱吧,
你敲家伙,
我道白,
扬起你的歌喉,兄弟,
泛起你的酒窝呀,朋友!
我们唱出黄河的愤怒,
唱出黄河的悲哀,
让我们集体的歌声
和黄河融合起来!
唱吧,
我们的歌声
不叫敌人过黄河!
唱吧,
我们的歌声
不许我们周围有破坏者!
我们不停息地唱,
我们不停息地歌,
直到这北方的巨流——
属于工人的河,
属于农民的河,
属于学生旅行的河,
属于青年人唱情歌的河,
属于将士胜利归来饮马的河……
那时候,我们站在河岸上
静静地听
黄河给我们唱
最动人
最快乐
最幸福的歌。







