Eigenfaces are a set of eigenvectors used in the computer vision problem of human face recognition. The approach of using eigenfaces for recognition was developed by Sirovich and Kirby (1987) and used by Matthew Turk and Alex Pentland in face classification. It is considered the first successful example of facial recognition technology.[citation needed] These eigenvectors are derived from the covariance matrix of the probability distribution of the high-dimensional vector space of possible faces of human beings.
Eigenface generation
To generate a set of eigenfaces, a large set of digitized images of human faces, taken under the same lighting conditions, are normalized to line up the eyes and mouths. They are then all resampled at the same pixel resolution. Eigenfaces can be extracted out of the image data by means of a mathematical tool called principal component analysis (PCA).
The eigenfaces that are created will appear as light and dark areas that are arranged in a specific pattern. This pattern is how different features of a face are singled out to be evaluated and scored. There will be a pattern to evaluate symmetry, if there is any style of facial hair, where the hairline is, or evaluate the size of the nose or mouth. Other eigenfaces have patterns that are less simple to identify, and the image of the eigenface may look very little like a face.
The technique used in creating eigenfaces and using them for recognition is also used outside of facial recognition. This technique is also used for handwriting analysis, lip reading, voice recognition, sign language/hand gestures and medical imaging. Therefore, some do not use the term eigenface, but prefer to use 'eigenimage'. Research that applies similar eigen techniques to sign language images has also been made.
Informally, eigenfaces are a set of "standardized face ingredients", derived from statistical analysis of many pictures of faces. Any human face can be considered to be a combination of these standard faces. For example, your face might be composed of the average face plus 10% from eigenface 1, 55% from eigenface 2, and even -3% from eigenface 3. Remarkably, it does not take many eigenfaces summed together to give a fair likeness of most faces. Also, because a person's face is no longer recorded by a digital photograph, but instead as just a list of values (one value for each eigenface in the database used), much less space is taken for each person's face.
Practical implementation
Here are the steps involved in creating a set of eigenfaces:
- Prepare a training set. The faces constituting the training set should be of prepared for processing, in the sense that they should all have the same resolution and that the faces should be roughly aligned. Each image is seen as one vector, simply by concatenating the rows of pixels in the original image. A greyscale image with r rows and c columns is therefore represented as a vector with r x c elements. In the following discussion we assume all images of the training set are stored in a single matrix T, where each row of the matrix is an image.
- Subtract the mean. The average image a has to be calculated and subtracted from each original image in T.
- Calculate the eigenvectors and eigenvalues of the covariance matrix S. Each eigenvector has the same dimensionality as the original images and can itself be seen as an image. The eigenvectors of this covariance matrix are therefore called eigenfaces. They are the directions in which the images in the training set differ from the mean image. In general this will be a computationally expensive step (when it is at all possible), but the practical applicability of eigenfaces stems from the possibility to compute the eigenvectors of S efficiently, without ever computing S explicitly, as detailed below.
- Choose the principal components. The D x D covariance matrix will result in D eigenvectors, each representing a direction in the image space. Keep the eigenvectors with largest associated eigenvalue.
The eigenfaces can now be used to represent new faces: we can project a new (mean-subtracted) image on the eigenfaces and thereby record how that new face differs from the mean face. The eigenvalues associated with each eigenface represent how much the images in the training set vary from the mean image in that direction. We lose information by projecting the image on a subset of the eigenvectors, but we minimise this loss by keeping those eigenfaces with the largest eigenvalues. For instance, if we are working with a 100 x 100 image, then we will obtain 10,000 eigenvectors. In practical applications, most faces can typically be identified using a projection on between 100 and 150 eigenfaces, so that most of the 10,000 eigenvectors can be discarded.
Computing the eigenvectors
Performing PCA directly on the covariance matrix of the images is often computationally infeasible. If small, say 100 x 100, greyscale images are used, each image is a point in a 10,000-dimensional space and the covariance matrix S is a matrix of 10,000 x 10,000 = 108 elements. However the rank of the covariance matrix is limited by the number of training examples: if there are N training examples, there will be at most N-1 eigenvectors with non-zero eigenvalues. If the number of training examples is smaller than the dimensionality of the images, the principal components can be computed more easily as follows.
Let T be the matrix of preprocessed training examples, where each row contains one mean-subtracted image. The covariance matrix can then be computed as S = TT T and the eigenvector decomposition of S is given by
However TTT is a large matrix, and if instead we take the eigenvalue decomposition of
then we notice that by pre-multiplying both sides of the equation with TT, we obtain
Meaning that, if ui is an eigenvector of TTT, then vi=TTui is an eigenvector of S. If we have a training set of 300 images of 100 x 100 pixels, the matrix TTT is a 300 x 300 matrix, which is much more manageable than the 10000 x 10000 covariance matrix. Notice however that the resulting vectors vi are not normalised; if normalisation is required it should be applied as an extra step.
Use in facial recognition
Facial recognition was the source of motivation behind the creation of eigenfaces. For this use, eigenfaces have advantages over other techniques available, such as the system's speed and efficiency. Using eigenfaces is very fast, and able to functionally operate on lots of faces in very little time. Unfortunately, this type of facial recognition does have a drawback to consider: trouble recognizing faces when they are viewed with different levels of light or angles. For the system to work well, the faces need to be seen from a frontal view under similar lighting. Face recognition using eigenfaces has been shown to be quite accurate. By experimenting with the system to test it under variations of certain conditions, the following correct recognitions were found: an average of 96% with light variation, 85% with orientation variation, and 64% with size variation. (Turk & Pentland 1991, p. 590)
To complement eigenfaces, another approach has been developed called eigenfeatures. This combines facial metrics (measuring distance between facial features) with the eigenface approach. Another method, which is competing with the eigenface technique uses 'fisherfaces'. This method for facial recognition is less sensitive to variation in lighting and pose of the face than the method using eigenfaces.
A more modern alternative to eigenfaces and fisherfaces is the active appearance model, which decouples the face's shape from its texture: it does an eigenface decomposition of the face after warping it to mean shape. This allows it to perform better on different projections of the face, and when the face is tilted.
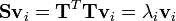

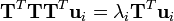




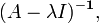


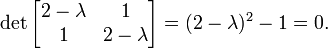
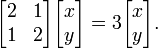


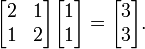 For the eigenvalue
For the eigenvalue