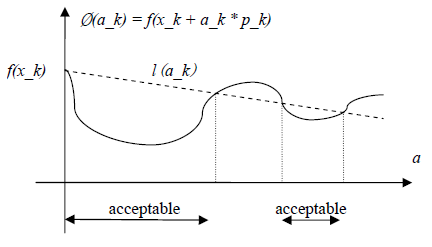
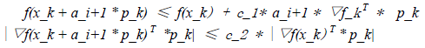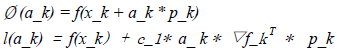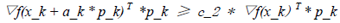The original link to the code is here
// ISO C9x compliant stdint.h for Microsoft Visual Studio // Based on ISO/IEC 9899:TC2 Committee draft (May 6, 2005) WG14/N1124 // // Copyright (c) 2006-2008 Alexander Chemeris // // Redistribution and use in source and binary forms, with or without // modification, are permitted provided that the following conditions are met: // // 1. Redistributions of source code must retain the above copyright notice, // this list of conditions and the following disclaimer. // // 2. Redistributions in binary form must reproduce the above copyright // notice, this list of conditions and the following disclaimer in the // documentation and/or other materials provided with the distribution. // // 3. The name of the author may be used to endorse or promote products // derived from this software without specific prior written permission. // // THIS SOFTWARE IS PROVIDED BY THE AUTHOR ``AS IS'' AND ANY EXPRESS OR IMPLIED // WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF // MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO // EVENT SHALL THE AUTHOR BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, // SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, // PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; // OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, // WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR // OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF // ADVISED OF THE POSSIBILITY OF SUCH DAMAGE. // /////////////////////////////////////////////////////////////////////////////// #ifndef _MSC_VER // [ #error "Use this header only with Microsoft Visual C++ compilers!" #endif // _MSC_VER ] #ifndef _MSC_STDINT_H_ // [ #define _MSC_STDINT_H_ #if _MSC_VER > 1000 #pragma once #endif #include// For Visual Studio 6 in C++ mode and for many Visual Studio versions when // compiling for ARM we should wrap include with 'extern "C++" {}' // or compiler give many errors like this: // error C2733: second C linkage of overloaded function 'wmemchr' not allowed #ifdef __cplusplus extern "C" { #endif # include #ifdef __cplusplus } #endif // Define _W64 macros to mark types changing their size, like intptr_t. #ifndef _W64 # if !defined(__midl) && (defined(_X86_) || defined(_M_IX86)) && _MSC_VER >= 1300 # define _W64 __w64 # else # define _W64 # endif #endif // 7.18.1 Integer types // 7.18.1.1 Exact-width integer types // Visual Studio 6 and Embedded Visual C++ 4 doesn't // realize that, e.g. char has the same size as __int8 // so we give up on __intX for them. #if (_MSC_VER < 1300) typedef signed char int8_t; typedef signed short int16_t; typedef signed int int32_t; typedef unsigned char uint8_t; typedef unsigned short uint16_t; typedef unsigned int uint32_t; #else typedef signed __int8 int8_t; typedef signed __int16 int16_t; typedef signed __int32 int32_t; typedef unsigned __int8 uint8_t; typedef unsigned __int16 uint16_t; typedef unsigned __int32 uint32_t; #endif typedef signed __int64 int64_t; typedef unsigned __int64 uint64_t; // 7.18.1.2 Minimum-width integer types typedef int8_t int_least8_t; typedef int16_t int_least16_t; typedef int32_t int_least32_t; typedef int64_t int_least64_t; typedef uint8_t uint_least8_t; typedef uint16_t uint_least16_t; typedef uint32_t uint_least32_t; typedef uint64_t uint_least64_t; // 7.18.1.3 Fastest minimum-width integer types typedef int8_t int_fast8_t; typedef int16_t int_fast16_t; typedef int32_t int_fast32_t; typedef int64_t int_fast64_t; typedef uint8_t uint_fast8_t; typedef uint16_t uint_fast16_t; typedef uint32_t uint_fast32_t; typedef uint64_t uint_fast64_t; // 7.18.1.4 Integer types capable of holding object pointers #ifdef _WIN64 // [ typedef signed __int64 intptr_t; typedef unsigned __int64 uintptr_t; #else // _WIN64 ][ typedef _W64 signed int intptr_t; typedef _W64 unsigned int uintptr_t; #endif // _WIN64 ] // 7.18.1.5 Greatest-width integer types typedef int64_t intmax_t; typedef uint64_t uintmax_t; // 7.18.2 Limits of specified-width integer types #if !defined(__cplusplus) || defined(__STDC_LIMIT_MACROS) // [ See footnote 220 at page 257 and footnote 221 at page 259 // 7.18.2.1 Limits of exact-width integer types #define INT8_MIN ((int8_t)_I8_MIN) #define INT8_MAX _I8_MAX #define INT16_MIN ((int16_t)_I16_MIN) #define INT16_MAX _I16_MAX #define INT32_MIN ((int32_t)_I32_MIN) #define INT32_MAX _I32_MAX #define INT64_MIN ((int64_t)_I64_MIN) #define INT64_MAX _I64_MAX #define UINT8_MAX _UI8_MAX #define UINT16_MAX _UI16_MAX #define UINT32_MAX _UI32_MAX #define UINT64_MAX _UI64_MAX // 7.18.2.2 Limits of minimum-width integer types #define INT_LEAST8_MIN INT8_MIN #define INT_LEAST8_MAX INT8_MAX #define INT_LEAST16_MIN INT16_MIN #define INT_LEAST16_MAX INT16_MAX #define INT_LEAST32_MIN INT32_MIN #define INT_LEAST32_MAX INT32_MAX #define INT_LEAST64_MIN INT64_MIN #define INT_LEAST64_MAX INT64_MAX #define UINT_LEAST8_MAX UINT8_MAX #define UINT_LEAST16_MAX UINT16_MAX #define UINT_LEAST32_MAX UINT32_MAX #define UINT_LEAST64_MAX UINT64_MAX // 7.18.2.3 Limits of fastest minimum-width integer types #define INT_FAST8_MIN INT8_MIN #define INT_FAST8_MAX INT8_MAX #define INT_FAST16_MIN INT16_MIN #define INT_FAST16_MAX INT16_MAX #define INT_FAST32_MIN INT32_MIN #define INT_FAST32_MAX INT32_MAX #define INT_FAST64_MIN INT64_MIN #define INT_FAST64_MAX INT64_MAX #define UINT_FAST8_MAX UINT8_MAX #define UINT_FAST16_MAX UINT16_MAX #define UINT_FAST32_MAX UINT32_MAX #define UINT_FAST64_MAX UINT64_MAX // 7.18.2.4 Limits of integer types capable of holding object pointers #ifdef _WIN64 // [ # define INTPTR_MIN INT64_MIN # define INTPTR_MAX INT64_MAX # define UINTPTR_MAX UINT64_MAX #else // _WIN64 ][ # define INTPTR_MIN INT32_MIN # define INTPTR_MAX INT32_MAX # define UINTPTR_MAX UINT32_MAX #endif // _WIN64 ] // 7.18.2.5 Limits of greatest-width integer types #define INTMAX_MIN INT64_MIN #define INTMAX_MAX INT64_MAX #define UINTMAX_MAX UINT64_MAX // 7.18.3 Limits of other integer types #ifdef _WIN64 // [ # define PTRDIFF_MIN _I64_MIN # define PTRDIFF_MAX _I64_MAX #else // _WIN64 ][ # define PTRDIFF_MIN _I32_MIN # define PTRDIFF_MAX _I32_MAX #endif // _WIN64 ] #define SIG_ATOMIC_MIN INT_MIN #define SIG_ATOMIC_MAX INT_MAX #ifndef SIZE_MAX // [ # ifdef _WIN64 // [ # define SIZE_MAX _UI64_MAX # else // _WIN64 ][ # define SIZE_MAX _UI32_MAX # endif // _WIN64 ] #endif // SIZE_MAX ] // WCHAR_MIN and WCHAR_MAX are also defined in #ifndef WCHAR_MIN // [ # define WCHAR_MIN 0 #endif // WCHAR_MIN ] #ifndef WCHAR_MAX // [ # define WCHAR_MAX _UI16_MAX #endif // WCHAR_MAX ] #define WINT_MIN 0 #define WINT_MAX _UI16_MAX #endif // __STDC_LIMIT_MACROS ] // 7.18.4 Limits of other integer types #if !defined(__cplusplus) || defined(__STDC_CONSTANT_MACROS) // [ See footnote 224 at page 260 // 7.18.4.1 Macros for minimum-width integer constants #define INT8_C(val) val##i8 #define INT16_C(val) val##i16 #define INT32_C(val) val##i32 #define INT64_C(val) val##i64 #define UINT8_C(val) val##ui8 #define UINT16_C(val) val##ui16 #define UINT32_C(val) val##ui32 #define UINT64_C(val) val##ui64 // 7.18.4.2 Macros for greatest-width integer constants #define INTMAX_C INT64_C #define UINTMAX_C UINT64_C #endif // __STDC_CONSTANT_MACROS ] #endif // _MSC_STDINT_H_ ]
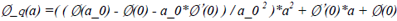
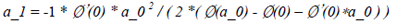
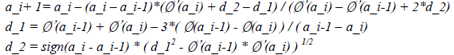
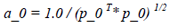
 a_i
a_i