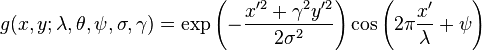在图形识别方面,主成分分析(Principal Comonents Analysis,PCA)算是比较快速而且又准确的方式之一,它可以对抗图形平移旋转的事件发生,并且藉由主要特征(主成分)投影过后的数据做数据的比对,在多个特征信息里面,取最主要的K个,做为它的特征依据,在这边拿前面共变量矩阵的数据来做沿用,主成分分析使用的方法为计算共变量矩阵,在加上计算共变量矩阵的特征值及特征向量,将特征值以及所对应的特征向量排序之后,取前面主要K个特征向量当做主要特征,而OpenCV也可以对高维度的向量进行主成分分析的计算。
| x | 1.5 | 3.0 | 1.2 | 2.1 | 3.1 | 1.3 | 2.0 | 1.0 | 0.5 | 1.0 |
| y | 2.3 | 1.7 | 2.9 | 2.2 | 3.1 | 2.7 | 1.7 | 2.0 | 0.6 | 0.9 |
数据原始的分布情况,红点代表着它的平均数

将坐标系位移,以红点为主要的原点

计算共变量矩阵以及共变量的特征值以及特征向量,将特征向量排序后投影回原始数据的结果的结果,也就是说,对照上面的图片,EigenVector的作用是找到主轴后,将原本的坐标系做旋转了

再来就是对它做投影,也就是降低维度的动作,将Y轴的数据全部归零,投影在X轴上

投影完之后,在将它转回原本的坐标系

PCA主成分分析,与线性回归有异曲同工之妙,也就是说,这条投影过后的直线,可以称做回归线,当它在做主轴旋转的时候,所投影的结果为最小均方误,在将它转置回来的时候,就形成了一条回归直线了
OpenCV的PCA输入必须要是单信道32位浮点数格式或是单信道64位浮点数格式的,参数为CV_32FC1或是CV_64FC1,程序写法如下
PCA程序实作
#include <cv.h>
#include <highgui.h>
#include <stdio.h>
#include <stdlib.h>
float Coordinates[20]={1.5,2.3,
3.0,1.7,
1.2,2.9,
2.1,2.2,
3.1,3.1,
1.3,2.7,
2.0,1.7,
1.0,2.0,
0.5,0.6,
1.0,0.9};
void PrintMatrix(CvMat *Matrix,int Rows,int Cols);
int main()
{
CvMat *Vector1;
CvMat *AvgVector;
CvMat *EigenValue_Row;
CvMat *EigenVector;
Vector1=cvCreateMat(10,2,CV_32FC1);
cvSetData(Vector1,Coordinates,Vector1->step);
AvgVector=cvCreateMat(1,2,CV_32FC1);
EigenValue_Row=cvCreateMat(2,1,CV_32FC1);
EigenVector=cvCreateMat(2,2,CV_32FC1);
cvCalcPCA(Vector1,AvgVector,EigenValue_Row,EigenVector,CV_PCA_DATA_AS_ROW);
printf("Original Data:\n");
PrintMatrix(Vector1,10,2);
printf("==========\n");
PrintMatrix(AvgVector,1,2);
printf("\nEigne Value:\n");
PrintMatrix(EigenValue_Row,2,1);
printf("\nEigne Vector:\n");
PrintMatrix(EigenVector,2,2);
system("pause");
}
void PrintMatrix(CvMat *Matrix,int Rows,int Cols)
{
for(int i=0;i<Rows;i++)
{
for(int j=0;j<Cols;j++)
{
printf("%.2f ",cvGet2D(Matrix,i,j).val[0]);
}
printf("\n");
}
}
细节分析
这部份是把平均数,共变量矩阵,以及特征值及特征向量都计算出来了,全部都包在cvCalcPCA()的函式里面,因此可以不必特地的用cvCalcCovarMatrix()求得共变量矩阵,也不需要再由共变量矩阵套用cvEigenVV()求得它的EigenValue以及EigenVector了,所以说,cvCalcPCA()=cvCalcCovarMatrix()+cvEigenVV(),不仅如此,cvCalcPCA()使用上更是灵活,当向量的维度数目比输入的数据大的时候(例如Eigenface),它的共变量矩阵就会自动转成CV_COVAR_SCRAMBLED,而当输入数据量比向量维度大的时候,它亦会自动转成CV_COVAR_NORMAL的形态,而OpenCV也提供了计算投影量cvProjectPCA(),以及反向投影的函式cvBackProjectPCA(),cvCalcPCA()的计算结果如下

详细计算方法可以参考"OpenCV统计应用-共变量矩阵"以及"OpenCV线性代数-cvEigenVV实作"这两篇,cvCalcPCA()第一个自变量为输入目标要计算的向量,整合在CvMat数据结构里,第二个自变量为空的平均数向量,第三个自变量为输出排序后的EigenValue,以列(Rows)为主的数值,第四个自变量为排序后的EigenVector,第五个自变量为cvCalcPCA()的参数,它的参数公式如下
#define CV_PCA_DATA_AS_ROW 0
#define CV_PCA_DATA_AS_COL 1
#define CV_PCA_USE_AVG 2
分别代表以列为主,以栏为主的参数设定,以及使用自己定义的平均数,CV_PCA_DATA_AS_ROW与CV_PCA_DATA_AS_COL的参数不可以同时使用,而对于主成分分析的EigenVector对原始数据投影的程序范例如下
PCA特征向量投影
cvProjectPCA(),它的公式定义如下

因此,它所呈现的结果就是将坐标旋转后的特征向量投影,cvProjectPCA()的地一个自变量为输入原始向量数据,第二个自变量为输入空的(或是以设定好的)平均数向量,第三个自变量为输入以排序好的特征向量EigenVector,第四个自变量为输出目标投影向量,而投影之外,OpenCV还可以给他做反向投影回原始的数据
PCA反向投影
#include <cv.h>
#include <highgui.h>
#include <stdio.h>
#include <stdlib.h>
float Coordinates[20]={1.5,2.3,
3.0,1.7,
1.2,2.9,
2.1,2.2,
3.1,3.1,
1.3,2.7,
2.0,1.7,
1.0,2.0,
0.5,0.6,
1.0,0.9};
int main()
{
CvMat *Vector1;
CvMat *AvgVector;
IplImage *Image1=cvCreateImage(cvSize(450,450),IPL_DEPTH_8U,3);
Image1->origin=1;
Vector1=cvCreateMat(10,2,CV_32FC1);
cvSetData(Vector1,Coordinates,Vector1->step);
AvgVector=cvCreateMat(1,2,CV_32FC1);
CvMat *EigenValue_Row=cvCreateMat(2,1,CV_32FC1);
CvMat *EigenVector=cvCreateMat(2,2,CV_32FC1);
cvCalcPCA(Vector1,AvgVector,EigenValue_Row,EigenVector,CV_PCA_DATA_AS_ROW);
cvProjectPCA(Vector1,AvgVector,EigenVector,Vector1);
cvBackProjectPCA(Vector1,AvgVector,EigenVector,Vector1);
printf("Back Project Original Data:\n");
for(int i=0;i<10;i++)
{
printf("%.2f ",cvGetReal2D(Vector1,i,0));
printf("%.2f ",cvGetReal2D(Vector1,i,1));
cvCircle(Image1,cvPoint((int)(cvGetReal2D(Vector1,i,0)*100),(int)(cvGetReal2D(Vector1,i,1)*100)),0,CV_RGB(0,0,255),10,CV_AA,0);
printf("\n");
}
cvCircle(Image1,cvPoint((int)((cvGetReal2D(AvgVector,0,0))*100),(int)((cvGetReal2D(AvgVector,0,1))*100)),0,CV_RGB(255,0,0),10,CV_AA,0);
printf("==========\n");
printf("%.2f ",cvGetReal2D(AvgVector,0,0));
printf("%.2f ",cvGetReal2D(AvgVector,0,1));
cvNamedWindow("Coordinates",1);
cvShowImage("Coordinates",Image1);
cvWaitKey(0);
}
执行结果:

而反向投影,只不过是将投影向量还原成原始数据罢了,可以用来做为新进数据反向投影后用来比对的步骤,以下是它的计算公式推导

cvBackProjectPCA()的自变量输入与cvProjectPCA()是一样的,只不过是里面的计算公式不同,其实也只是cvProjectPCA()的反运算
cvCalcPCA()
计算多笔高维度数据的主要特征值及特征向量,先自动判断维度大于数据量或维度小于数据量来选择共变量矩阵的样式,在由共变量矩阵求得已排序后的特征值及特征向量,cvCalcPCA()函式的参数为CV_PCA_DATA_AS_ROW以列为主的资料排列,CV_PCA_DATA_AS_COL以行为主的数据排列,CV_PCA_USE_AVG自行定义平均数数据,CV_PCA_DATA_AS_ROW以及CV_PCA_DATA_AS_COL不可以同时使用,cvCalcPCA()的第一个自变量为输入CvMat维度向量数据结构,第二个自变量为输入空的CvMat平均数向量数据结构(或是自行定义平均数向量),第三个自变量为输入以列为主的特征值CvMat数据结构,第四个自变量为输入特征向量CvMat数据结构,第四个自变量为输入cvCalcPCA()函式的参数
cvCalcPCA(输入目标向量数据CvMat数据结构,输入或输出向量平均数CvMat数据结构,输入以列为主EigenValue的CvMat数据结构,输入EigenVector的CvMat数据结构,目标参数或代号)
cvProjectPCA()
将计算主成分分析的结果做投影的运算,主要作用是将最具意义的k个EgienVector与位移后的原始资料做矩阵乘法,投影过后的结果将会降低维度,cvProjectPCA()第一个自变量为输入CvMat数据结构原始向量数据数据,第二个自变量为输入CvMat数据结构平均数向量,第三个自变量为输入要降维的特征向量,第四个自变量为输出CvMat数据结构原始数据投影的结果
cvProjectPCA(输入CvMat原始向量数据数据结构,输入CvMat原始向量平均数数据结构,输入CvMat降低维度的特征向量数据结构,输出CvMat投影向量数据结构)
cvBackProjectPCA()
将投影向量转回原始向量维度坐标系,cvProjectPCA()第一个自变量为输入CvMat数据结构投影向量数据,第二个自变量为输入CvMat数据结构平均数向量,第三个自变量为输入特征向量,第四个自变量为输出CvMat数据结构反向投影的结果
cvProjectPCA(输入CvMat投影向量数据结构,输入CvMat原始向量平均数数据结构,输入CvMat特征向量数据结构,输出CvMat反向投影数据结构)