A Gabor filter is a linear filter whose impulse response is defined by a harmonic function multiplied by a Gaussian function. Because of the multiplication-convolution property (Convolution theorem), the Fourier transform of a Gabor filter's impulse response is the convolution of the Fourier transform of the harmonic function and the Fourier transform of the Gaussian function.
where
and
In this equation, λ represents the wavelength of the cosine factor, θ represents the orientation of the normal to the parallel stripes of a Gabor function, ψ is the phase offset, σ is the sigma of the Gaussian envelope and γ is the spatial aspect ratio, and specifies the ellipticity of the support of the Gabor function.
This is an example implementation in MATLAB:
function gb=gabor_fn(sigma,theta,lambda,psi,gamma) sigma_x = sigma; sigma_y = sigma/gamma; sz_x=fix(6*sigma_x); if mod(sz_x,2)==0, sz_x=sz_x+1;end sz_y=fix(6*sigma_y); if mod(sz_y,2)==0, sz_y=sz_y+1;end [x y]=meshgrid(-fix(sz_x/2):fix(sz_x/2),fix(-sz_y/2):fix(sz_y/2)); % Rotation x_theta=x*cos(theta)+y*sin(theta); y_theta=-x*sin(theta)+y*cos(theta); gb=exp(-.5*(x_theta.^2/sigma_x^2+y_theta.^2/sigma_y^2)).*cos(2*pi/lambda*x_theta+psi);
Gabor filters are directly related to Gabor wavelets, since they can be designed for number of dilations and rotations. However, in general, expansion is not applied for Gabor wavelets, since this requires computation of biorthogonal wavelets, which may be very time-consuming. Therefore, usually, a filter bank consisting of Gabor filters with various scales and rotations is created. The filters are convolved with the signal, resulting in a so-called Gabor space. This process is closely related to processes in the primary visual cortex (Daugman, 1980). The Gabor space is very useful in e.g., image processing applications such as iris recognition and fingerprint recognition. Relations between activations for a specific spatial location are very distinctive between objects in an image. Furthermore, important activations can be extracted from the Gabor space in order to create a sparse object representation.
To visualize a 2-dimensional Gabor filter and the resulting activations after convolving it with an image, the on-line Gabor application on http://matlabserver.cs.rug.nl can be useful.
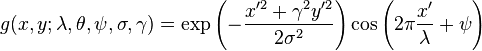


No comments:
Post a Comment