Unconstrained optimization

NOTE: this article is based on a serial blog from 52nlp.cn written by “jianzhu”. I translated from the Chinese version but there are not exactly the same. The original link to the blogs is attached: Click here. 

1. What is unconstrained optimization problem.

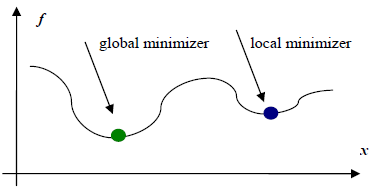
The above image shown an example of unconstrained optimization problem. Suppose we have function, called f, and its plot in 2D space is as above. Unconstrained optimization is a process that tries to find the minimum point(s) of f. In the figure above, there are two minimum points, one is global minimum(or minimal point) and the other one is a local minimum. As the limitation of the complexity of the algorithm, most unconstraint optimizer algorithms could only guarantee a local minimum. If we could only find local minimum, why we could still apply those “not-so-good” algorithms to solve our problems? From my point of view, there are mainly two reasons, the first is that many problems we are facing are modeled as a convex function, which means that the minimum and minimal are the same point; the second reason is that our world is not perfect, local minimum may sufficient for us in some cases.

Now we have known what is the unconstraint optimization problem, let us work on the basic process of unconstraint optimization. The first thing we have to do is to find an initial point, denoted as a red dot. Sometimes we randomly choose that point, sometimes we guess it with some heuristics, the rest of the time we could calculate it. It is all depended on what is your problem.

 

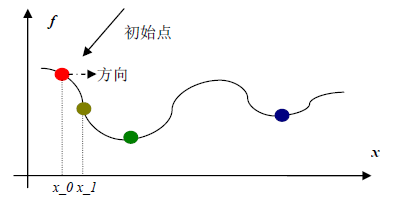
After we have the initial point, we could begin a arbitrary optimization algorithm to find the minimum point. During the optimizing, two concepts are critical, direction and step size.

2. Line search

Line search is used to calculate the step size, which mentioned above. Once we find the direction, we need to find how far we should move from current point, x_k and stop at the next “proper” point, x_(k+1). If we use p_k to denote the direction from the k-th point to the (k+1)-th point, x_k denotes current point, x_(k+1) denotes the nect point, and a_k denotes the k-th step size, then the following equation holds:

x_(k+1) = x_k + a_k * p_k

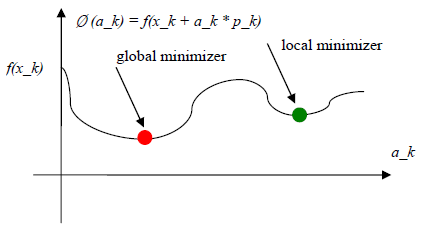
In most line search method, p_k should be the decent direction, which means f(x) would decrease if we move along p_k. As the goal is to find a minimum value, the best situation is that find a a_k that satisfies f(x_(k+1)) is the global minimum along p_k. The following equation shows the best situation:

Ø (a_k) = f(x_k+1) = f(x_k + a_k * p_k)

If we want to find a step size that makes Ø (a_k) to be global minimum, a great amount of calculation related to f(x_k+a_k*p_k); on the other hand, if we consider this problem from derivative point of view, we have to calculate ▽f_k+1, which is also unrealistic. So, we have to make some tradeoff between computation load and problem solving.

If we cannot build Roma in one day, what we should do with a_k? We give two constraints to determine what is a reasonable a_k and what is the size of a_k.

 

To be continued.