choosing step size
After we understand the meaning of Wolfe Condition, we have had an metric to measure what is good step size, and then, we could begin to find good step size based on this metric. When line search is trying to calculate the step size, a_k, an initial point, a_0, is needed, and then generate a serial points, {a_i}, until a_I satisfies Wolfe condition. Once a step size is selected, it becomes the next a_i. In this blog, I would mainly introduce two commonly used strategies, square interpolation and cubic interpolation.
Square/Cubic interpolation
When given an initial step size, a_0, if this step size satisfies Wolfe conditions, then a_0 becomes a_k, which means the calculation at x_k is terminated. Otherwise, we could use the information, Ø(a_0)、Ø(0)、Ø’(0), at this position to build a 2-order interpolating polynomial to fit Ø(a_k). This polynomial is as followed: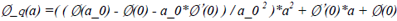
After reviewing the equation above, we could find that it satisfies the following conditions:
Ø_q(0) = Ø(0) Ø_q’(0) = Ø’(0) Ø_q(a_0) = Ø(a_0)
Then we calculate the derivative of the above equation and make it to be zero, which means we have found the value of a that leading to minimum.
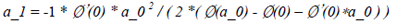
If a_I satisfies Wolfe condition, a_k is set to a_1. Otherwise, we would build a 3-order interpolation polynomial and try to find a that leads to minimum value. The process of this interpolation are shown as following: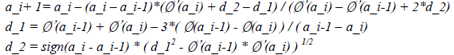
If a_(i+1) satisfies Wolfe condition, the a_k is set to a_(i+1). Otherwise, we continue the above procedure, and use Ø (a_i+1) and Ø’(a_i+1) to replace the value at a_(i-1) and a_i. Once one of a_(i-1) and a_i is set, we use the new value to replace corresponding value. This procedure would be continued until find a value satisfies the Wolfe condition, or not point found.
In Newton method, or Quasi-Newton method, the initial step size is 1, which could ensure that whatever step size we select is unit step size and make a fast converging speed. When calculating the first step size, a-0, we use the following equation to calculate: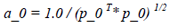
In the following steps, a_0 is always 1.
Calculating a_k
In this section, we would make a summer on the step size calculation with details. Suppose x_k is current point, and we want to find a step size satisfies Wolfe Condition, and move the current position to x_(k+1). We choose the initial point a_0 = 1. Then:
1) initialize a_x <- a_y <- 0Ø(a_x) 、 Ø(a_y) 、Ø’(a_x) 、 Ø’(a_y)、a_min、a_max
2) initialize a_I <- a_o, Ø’(a_i)、Ø(a_i)
3) if Ø(a_i) > Ø(a_x). This means a_I is too big. So the proper step size must be between [a_x a_i]. By using square and cubic interpolation on a_x and a_I, get two new step size, a_quadratic and a_cubic, and use the one near a_x as the step size. Here assuming use the new step size to overwrite a_quaratic, and apply the following operations:
a_y
a_i
Ø(a_y)Ø(a_i)
Ø’(a_y)Ø’(a_i)
a_i+1a_quadrati
In this case, a_k is in the interval of a_x and a_y.
4) If Ø’(a_i)* Ø’(a_x) < 0, a_I is too big. So the step size must be in the interval of [a_x a_i]. After interpolation, we use the step size which close to a_i. And do the following operations:
a_y
a_x
Ø(a_y)Ø(a_x)
Ø’(a_y)Ø’(a_x)
a_x
a_i
Ø(a_x)Ø(a_i)
Ø’(a_x)Ø’(a_i)
a_i+1
a_quadratic
5) |Ø’(a_i)| <|Ø’(a_x) |, which means the step size is too small. After interpolation, we do the following operations:
a_x
a_i
Ø(a_x)Ø(a_i)
Ø’(a_x)Ø’(a_i)
a_i+1
a_quadrati
6) if |Ø’(a_i)| ≥|Ø’(a_x) |, a_I is too small. If we have already known the range of a_k, such as [a_x a_y], the good step size should be in [a_I a_y]. Then apply cubic interpolation on a_I and a_y, and set the new step size as a_cubic; otherwise, if a_x is smaller than a_I, which means the new step size is not big enough. So size the new step size should be a_max. If a_x > a_I, this means the new step size is not small enough, we should set it to a_min. And apply the following operations:
a_x
a_i
Ø(a_x)Ø(a_i)
Ø’(a_x)Ø’(a_i)
If we have known the interval, [a_x, a_y], of a_k, then
a_i+1
a_cubic
else if a_x < a_i
a_i+1a_max
else if a_x ≥ a_i
a_i+1a_min
7) if a_(i+1) satisfies the following conditions:
we set the new step size as a_(i+1) and end the process of calculating the step size.
Otherwise, go to 2) and continue the next iteration.
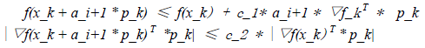
No comments:
Post a Comment