In computer vision, Difference of Gaussians is a grayscale image enhancement algorithm that involves the subtraction of one blurred version of an original grayscale image from another, less blurred version of the original. The blurred images are obtained by convolving the original grayscale image with Gaussian kernels having differing standard deviations. Blurring an image using a Gaussian kernel suppresses only high-frequency spatial information. Subtracting one image from the other preserves spatial information that lies between the range of frequencies that are preserved in the two blurred images. Thus, the difference of Gaussians is equivalent to a band-pass filter that discards all but a handful of spatial frequencies that are present in the original grayscale image.[1]
Mathematics of Difference of Gaussians
The Difference of Gaussians (DOG) is a wavelet mother function of null total sum which approximates the Mexican Hat wavelet by subtracting a wide Gaussian from a narrow Gaussian, as defined by this formula in one dimension:

and for the centered two-dimensional case (see Gaussian blur):
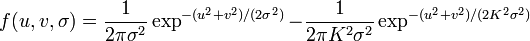
Details and applications
As an image enhancement algorithm, the Difference of Gaussians can be utilized to increase the visibility of edges and other detail present in a digital image. A wide variety of alternative edge sharpening filters operate by enhancing high frequency detail, but because random noise also has a high spatial frequency, many of these sharpening filters tend to enhance noise, which can be an undesirable artifact. The Difference of Gaussians algorithm removes high frequency detail that often includes random noise, rendering this approach one of the most suitable for processing images with a high degree of noise. A major drawback to application of the algorithm is an inherent reduction in overall image contrast produced by the operation.[1]
When utilized for image enhancement, the Difference of Gaussians algorithm is typically applied when the size ratio of kernel (2) to kernel (1) is 4:1 or 5:1. In the example images to the right, the sizes of the Gaussian kernels employed to smooth the sample image were 10 pixels and 5 pixels. The algorithm can also be used to obtain an approximation of the Laplacian of Gaussian when the ratio of size 2 to size 1 is roughly equal to 1.6[2]. The Laplacian of Gaussian is useful for detecting edges that appear at various image scales or degrees of image focus. The exact values of sizes of the two kernels that are used to approximate the Laplacian of Gaussian will determine the scale of the difference image, which may appear blurry as a result.
Differences of Gaussians have also been used for blob detection in the scale-invariant feature transform. In fact, the DOG as the difference of two Multivariate normal distribution has always a total null sum and convolving it with a uniform signal generates no response. It approximates well a second derivate of Gaussian (Laplacian of Gaussian) with K~1.6 and the receptive fields of ganglion cells in the retina with K~5. It may easily be used in recursive schemes and is used as an operator in real-time algorithms for blob detection and automatic scale selection.
No comments:
Post a Comment